One method of calculating π using an infinite series is to employ the Leibniz series. The formula for the Leibniz series is as follows:

This series is an alternating series, where the sign of each term alternates, and the absolute value of the terms decreases. You can use the C programming language to write a program that calculates an approximation of π using the first N terms of this series.
Even though the computation is time-consuming, each iteration brings the result closer to the accurate value of Pi. After 500,000 iterations, it is possible to accurately calculate Pi up to 10 decimal places.
The formula is as follows:
π = (4/1) – (4/3) + (4/5) – (4/7) + (4/9) – (4/11) + (4/13) – (4/15) …
The algorithm for calculating π using an infinite series.
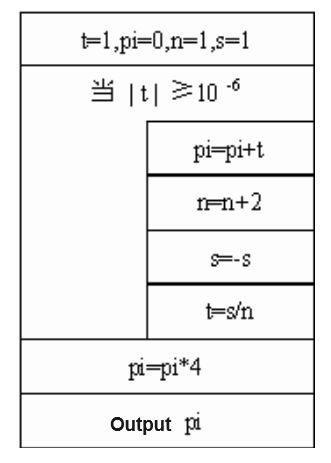
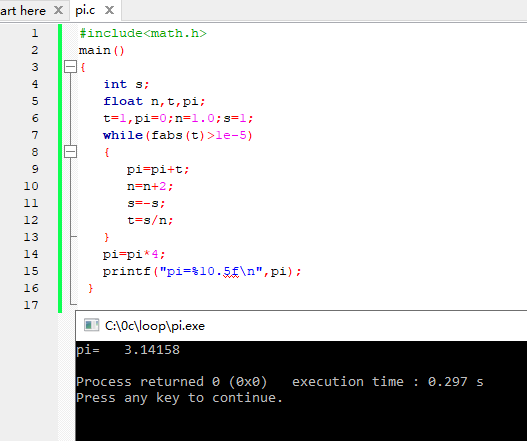
Example 1) Calculating π using an infinite series
#include<math.h>
main()
{
int s;
float n,t,pi;
t=1,pi=0;n=1.0;s=1;
while(fabs(t)>1e-5)
{
pi=pi+t;
n=n+2;
s=-s;
t=s/n;
}
pi=pi*4;
printf("pi=%10.5f\n",pi);
}
Output:
Example 2) Calculating π using the Leibniz series
#include <stdio.h>
// Function to calculate Pi using the Leibniz series
double calculatePiLeibniz(int n) {
double pi = 0.0;
int sign = 1;
for (int i = 0; i < n; i++) {
pi += sign / (2.0 * i + 1);
sign = -sign; // Switch the sign
}
return 4.0 * pi;
}
int main() {
int iterations = 500000; // Number of iterations
// Calculate Pi using the Leibniz series with 500,000 iterations
double approxPi = calculatePiLeibniz(iterations);
// Print the result with 10 decimal places
printf("Approximation of Pi using %d iterations: %.10f\n", iterations, approxPi);
return 0;
}
Output
Approximation of Pi using 500000 iterations: 3.1415926536
- The program defines a function
calculatePiLeibnizthat calculates π using the Leibniz series. It iteratesntimes, updating the value of π based on the series formula. - In the
mainfunction, the program setsiterationsto 500,000 and then calculates an approximation of π using the Leibniz series with this number of iterations. - The result is printed with 10 decimal places using
%.10fin theprintfstatement.
Note: The actual value of π is approximately 3.141592653589793, and the program’s output is a close approximation due to the Leibniz series iteration. Adjusting the number of iterations can improve precision at the expense of increased computation time.
