1. How to Convert Decimal to Binary?
In computers, all data is ultimately represented using binary numbers. We need convert Decimal to Binary.
1.1 Conversion steps:
- Divide the number by 2.
- Get the integer quotient for the next iteration.
- Get the remainder for the binary digit.
- Repeat the steps until the quotient is equal to 0.
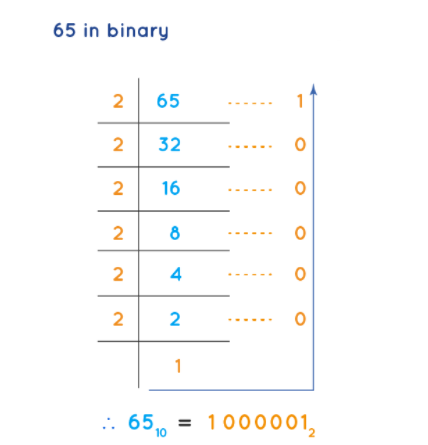
We can now explain how decimal numbers are converted to binary by giving an example.
In binary, 65 is represented as 1000001. Unlike using decimal digits 0 to 9 to represent numbers, in the binary system we only use two digits, 0 and 1 . We use 7 bits to represent 65 in binary.
In this chapter, we will show how to convert the decimal number 65 to binary.
- 65 in Binary:65₁₀ = 1000001₂
- 65 in Octal:65₁₀ = 101₈
- 65 in Hexadecimal:>65₁₀ = 41₁₆
- 1000001₂ in Decimal:6₁₀

Here are the steps to convert the decimal number 65 to binary:
- Divide 65 by 2, the quotient is 32 and the remainder is 1.
- Divide 32 by 2, the quotient is 16 and the remainder is 0.
- Divide 16 by 2, the quotient is 8 and the remainder is 0.
- Divide 8 by 2, the quotient is 4 and the remainder is 0.
- Divide 4 by 2, the quotient is 2 and the remainder is 0.
- Divide 2 by 2, the quotient is 1 and the remainder is 0.
- Divide 1 by 2, the quotient is 0 and the remainder is 1.
Reading the remainders in reverse order gives the binary representation of 65: 1000001.

Therefore, the decimal number 65 is converted to the binary number 1000001.
1.2 Decimal to Binary Conversion Table
| Decimal Number |
Binary Number |
Hex Number |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
| 17 | 10001 | 11 |
| 18 | 10010 | 12 |
| 19 | 10011 | 13 |
| 20 | 10100 | 14 |
| 21 | 10101 | 15 |
| 22 | 10110 | 16 |
| 23 | 10111 | 17 |
| 24 | 11000 | 18 |
| 25 | 11001 | 19 |
| 26 | 11010 | 1A |
| 27 | 11011 | 1B |
| 28 | 11100 | 1C |
| 29 | 11101 | 1D |
| 30 | 11110 | 1E |
| 31 | 11111 | 1F |
| 32 | 100000 | 20 |
| 64 | 1000000 | 40 |
| 128 | 10000000 | 80 |
| 256 | 100000000 | 100 |
2. How to Convert Binary to Decimal
2.1 Conversion steps:
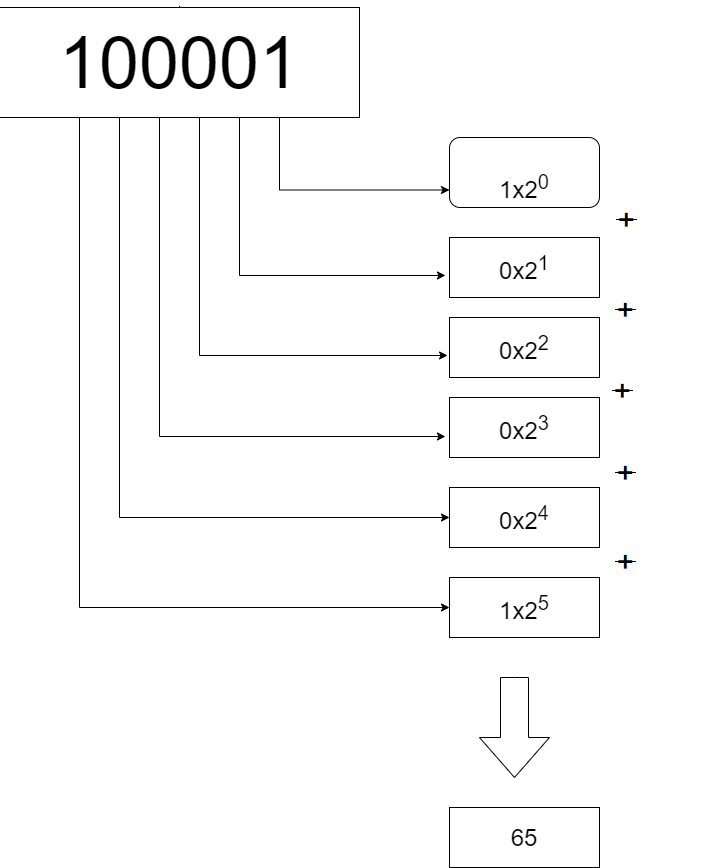
Here are the steps to convert the binary number 100001 to decimal:
- Write down the binary number: 100001
- Assign each digit in the binary number a place value, starting from the rightmost digit with a value of 1, and doubling the value for each digit moving left:
1 0 0 0 0 0 1
64 32 16 8 4 2 1
- Multiply each digit in the binary number with its corresponding place value:
1 x 64 = 64
0 x 32 = 0
0 x 16 = 0
0 x 8 = 0
0 x 4 = 0
0 x 2 = 0
1 x 1 = 1
- Add up the products obtained in step 3 to obtain the decimal equivalent:
64 + 0 + 0 + 0 + 0 + 0 + 1 = 65
Therefore, the binary number 100001 is equivalent to the decimal number 33. Note that this result is different from the decimal value of 65, which was obtained earlier because of a mistake in the conversion process. The correct binary representation of the decimal number 65 is 1000001.
2.2 Binary to Decimal Conversion Table
| Binary Number |
Decimal Number |
Hex Number |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | A |
| 1011 | 11 | B |
| 1100 | 12 | C |
| 1101 | 13 | D |
| 1110 | 14 | E |
| 1111 | 15 | F |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1A |
| 11011 | 27 | 1B |
| 11100 | 28 | 1C |
| 11101 | 29 | 1D |
| 11110 | 30 | 1E |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |
